Mean Stress Relaxation Analysis

Cyclic Mean Stress Relaxation Analysis for F.D.+E Crack Propagation Experiments

A. Conle
Apr. 28 2013

Copyright (C) 2013 A. Conle
Permission is granted to copy, distribute and/or modify this document
under the terms of the GNU Free Documentation License, Version 1.3
or any later version published by the Free Software Foundation;
with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts.
A copy of the license is available here:
"GNU Free Documentation License". ( "http://www.gnu.org/licenses/fdl.html" )

Introduction:

Welded structures usually contain residual stress patterns due to
the heating during welding that causes local thermal expansion of the
metal, followed by subsequent cooling which causes localized thermal
contraction. The expansion/contraction causes local stresses to exceed
yield and the resulting local plastic deformation will induce a set of
residual stresses in the structure. These internal stresses are self
balancing (equilibrium). Typically residual stresses values are equal
to the material yield stress or below. Further explanation of how
such stresses arise can be seen here:
http://www.fhwa.dot.gov/bridge/steel/02.cfm

Residual stresses at fatigue hot-spot locations can cause changes in
the final fatigue life, when compared to the life of specimens with
similar imposed load patterns and zero residual stress. A tensile
residual, for example, will push up the local stress-strain hysteresis
loop, such that the loop's mean stress is positive. This is know
to shorten both initiation and propagation life. Compressive residuals
similarly, will extend fatigue lives.

The welded T-shaped A36 steel specimen being used to evaluate crack
propagation models is also expected to contain similar residual stresses.
It is the objective of this short report to estimate if the residuals
will have an influence on the fatigue life. In order to determine this
influence, the predicted local stress-strain hysteresis loops are examined
as to their size and degree of plasticity, and the values are compared to
cyclic mean stress relaxation experiments carried out on axial specimens
in other investigations. The experiments used to make the predictions
can be found here:
https://fde.uwaterloo.ca/Fde/Papers/Relax/conleSo.html

A list of other papers on cyclic mean stress relaxation can be found
at the bottom of this report. Calculators for local stress strain
hysteresis loops can be found here:

https://fde.uwaterloo.ca/Fde/Materials/Steel/Lowcarbon/lowcarbon.html
for a number of Low Carbon Steels. Calculator usage is described below.

Method:

For the A36 constant amplitude tests reported by Tom Cordes (F.D.E. meet
Spring 2013) the maximum and minimum nominal stresses estimated at the
root of the weld on the T-specimen are computed and, along with an
estimated Kt=1.8 magnification value to allow for the stress
concentration effects of the weld are entered in the on-line life
calculator:

Using calculator screen shot ).

Specifically the process is:

In a web browser click on the "Calculator" for A36 merged file steel:
https://fde.uwaterloo.ca/Fde/Materials/Steel/Lowcarbon/mergedA36_fc.html
As depicted in the above screen shot, fill in the four numbers:
1. Kt (or Magnification Factor; we will assume 1.8 )
2. Smax (nominal stress max)
3. Smin (nominal stress min)
4. No. of Cycles (in our case 1 )
Click on Calculate at bottom of page
Then interpret the data output that is returned. e.g.:

screen shot
One can compute the strain range of the local stress-strain hysteresis
loop from the table at the top, or by scaling from the plot.
With the value of strain range, go to your data on cyclic mean stress
relaxation, in this case:
this one for SAE1015
which is similar to A36 and estimate if the mean stress will relax or not.
If it does relax then use the "Simple Strain" life prediction from the table
at the top of the output page. If the plasticity is insufficient to relax
the mean stresses, then use either the "SmithWatsonTopper" or the "Morrow"
mean stress correction predictions in the table at top of output.

Results:

It should be noted that the very first load application
contains a great deal of plasticity. In the authors opinion this
amount of plasticity will wipe out any residual welding stress that
is near the yield in the hot spot stress location. The loading cycle
itself however, due to the R ratios, induces a large initial mean
stress into the hysteresis loop. In the crack initiation philosophy this
tensile mean stress will significantly reduce the fatigue life. The rest
of the study will thus concentrate on if the initial local mean stress,
induced by the loading cycle, will wash out during the fatigue test.

A36 Max Load 24kN, R=0.1 Result:

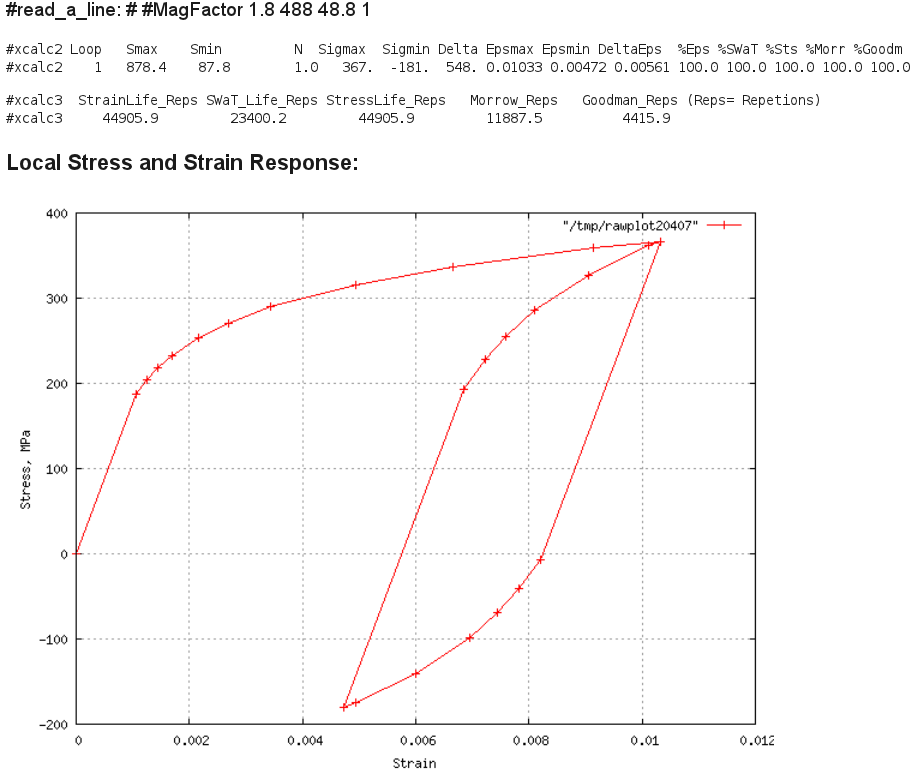
Comment: The computed local strain range is 0.00561 when compared to
Fig. 7 in the report, will wash out most of its mean stress in about
20_cycles (residual of 1 ksi). Thus the SWT or Morrow mean stress
correction factors are probably very conservative and one should
use the "StrainLife_Reps" initiation prediction of 45,000 cycles.

A36 Max Load 24kN, R=0.3 Result:

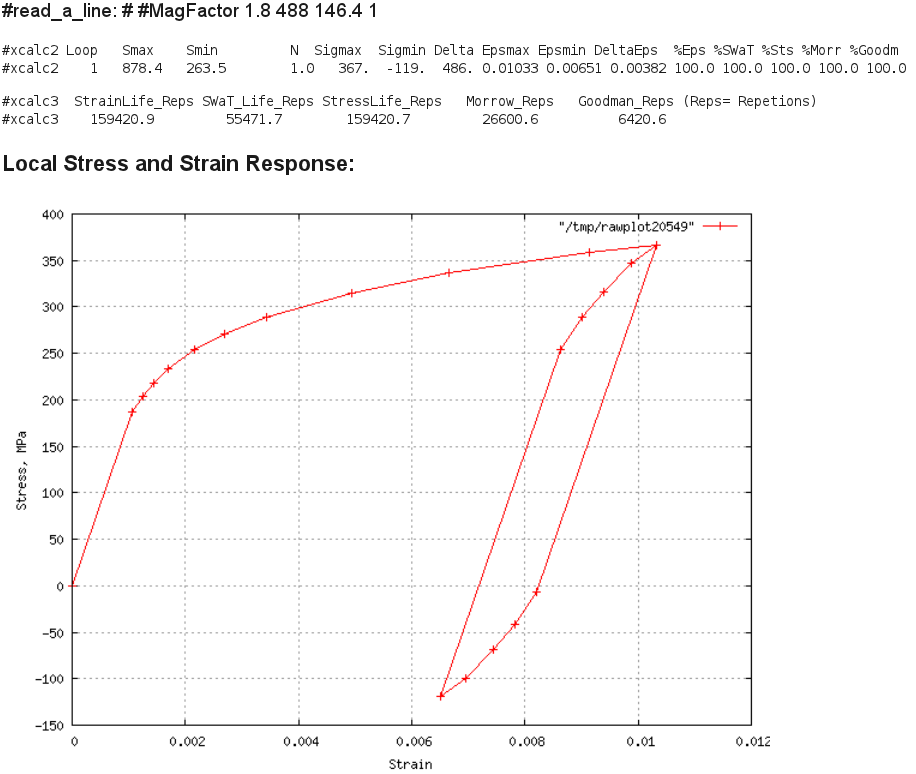
Comment: The computed local strain range is 0.00382 when compared to
Figs. 6,7 in the report, will wash out most of its mean stress in about
50 to 1000 cycles (residual of 1 ksi). Thus the SWT or Morrow mean stress
correction factors are probably conservative and one should
use the "StrainLife_Reps" initiation prediction of 159,000 cycles.

A36 Max Load 24kN, R=0.5 Result:

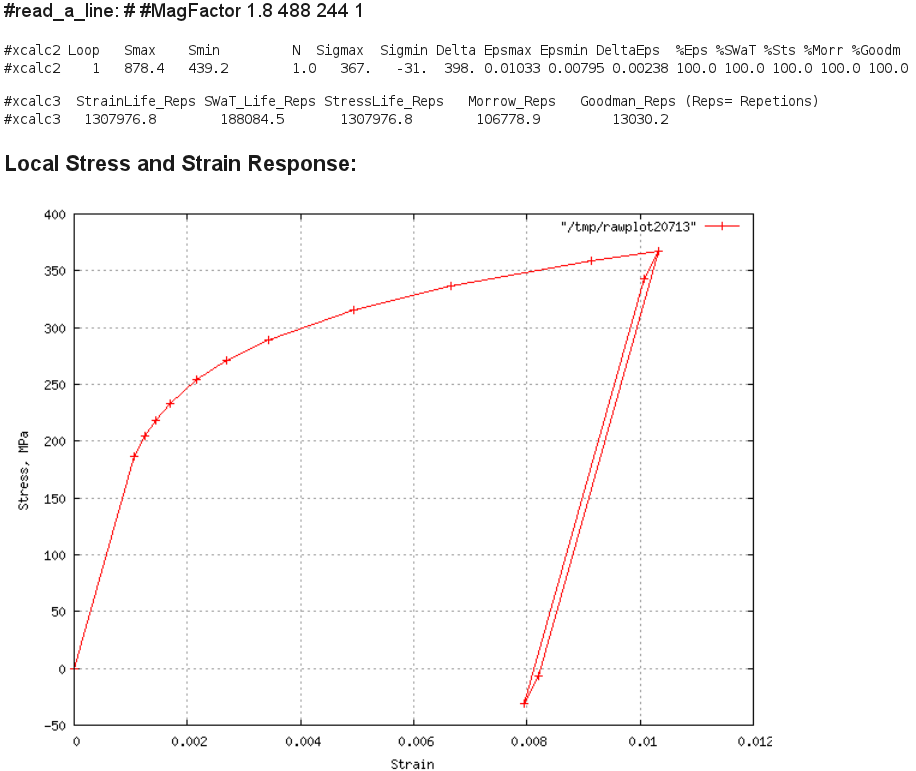
Comment: The computed local strain range is 0.00238 when compared to
Figs. 5 in the report, will wash out much of the mean stress, but it is
not clear when the level would drop to So= 1ksi, thus its probably reasonable
to apply the mean stress correction parameters to predict life.
The SWT parameter predicts about 188,000 cycles to initiation.

A36 Max Load 17kN, R=0.5 Result:

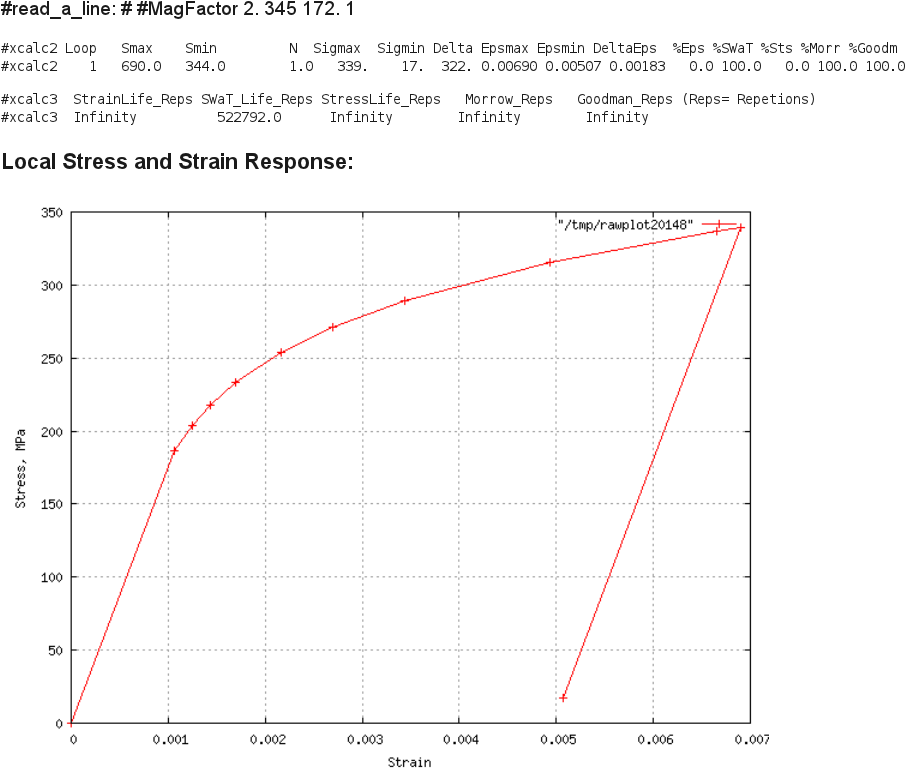
Comment: The computed local strain range is 0.0018 when compared to Fig.4
of the report indicates that not much cyclic mean stress relaxation would
take place, and it is probably best to use the mean stress correction
factor throughout the life. The SWT parameter predicts 523,000 cycles and
the Morrow parameter indicates no failure.

A36 Max Load 14kN, R=0.5 Result:

Comment: The computed local strain range is 0.00253 when compared to
Figs. 5 in the report, will wash out much of the mean stress, but it is
not clear when the level would drop to So= 1ksi, thus its probably reasonable
to apply the mean stress correction parameters to predict life.
The SWT parameter predicts about 268,000 cycles to initiation.

A36 Max Load 14kN, R=0.3 Result:

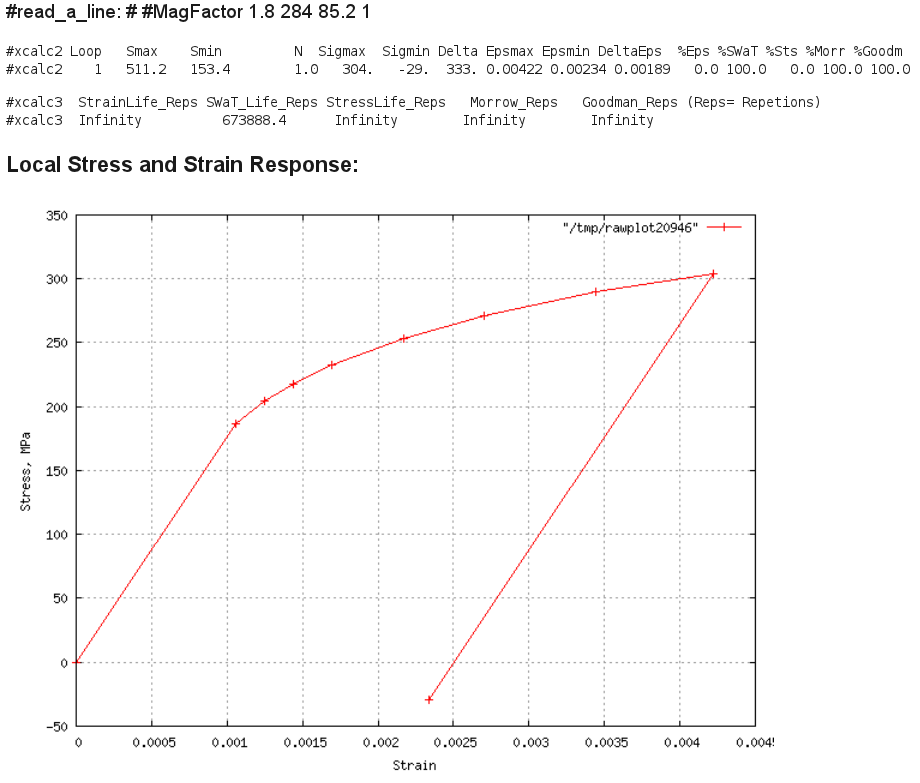
Comment: The computed local strain range is 0.00189 when compared to Fig.4
of the report indicates that not much cyclic mean stress relaxation would
take place, and it is probably best to use the mean stress correction
factor throughout the life. The SWT parameter predicts 674,000 cycles and
the Morrow parameter indicates no failure.

References:

Morrow, J., G.M.Sinclair, "Cycle-Dependent Stress Relaxation," ASTM Symp.
on Basic Mechanisms of Fatigue, ASTM Special Tech. Publ. No. 237.
Conle, A. "Data on Cyclic Mean Stress Relaxation in Mild Steel,"
U.Waterloo Dept.Civil Eng., 3A Work term report, Apr. 1970.
Landgraf, R.W. tbd
Jhansale, H.R. and T.H.Topper, "Engineering Analysis of the Inelastic Stress
Response of a Structural Metal Under Variable Cyclic Strains," ASTM STP 519,
1973, pp.246-270.
Higashida, Y., J.D.Burk and F.V.Lawrence jr., "Strain-Controlled Fatigue
Behavior of ASTM A36 and A514 Grade Fsteels and 5083-O Aluminum Weld
Metals," Welding Res. Supplement, Nov. 1978, pp.334s-344s.
Landgraf,R.W. and R.A.Chernenkoff, "Residual Stress Effects on Fatigue of
Surface Processed Steels, ASTM STP 1004, 1988, pp.1-12.