.
Other Links:
How to use cyclic stress relaxation data for fatigue life calculation.
Data on Cyclic Mean Stress Relaxation in Mild Steel
A.Conle
3A Civil Engr., April 1970
Converted to html Apr.2013
(Work Term Report for the Dept. of Co-ordination and Placement, University of Waterloo.)
Copyright (C) 2013 F.A. Conle
Permission is granted to copy, distribute and/or modify this document
under the terms of the GNU Free Documentation License, Version 1.3
or any later version published by the Free Software Foundation;
with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts.
A copy of the license is available here:
"GNU Free Documentation License".
( "http://www.gnu.org/licenses/fdl.html" )
Acknowledgment
The author is indebted to Professor T.H.Topper and H.R.Jhansale for their
supervision and guidance throughout the project, and to F.Andrewartha and
P.Watson for their stimulating discussions and advice on the subject of fatigue.
List of Symbols
- N Cycles
- Δε₁ Total strain range for block of cycles applied before
introduction of mean stress by a change in strain limits.
- Δε₂ Total strain range for block of cycles containing a mean stress
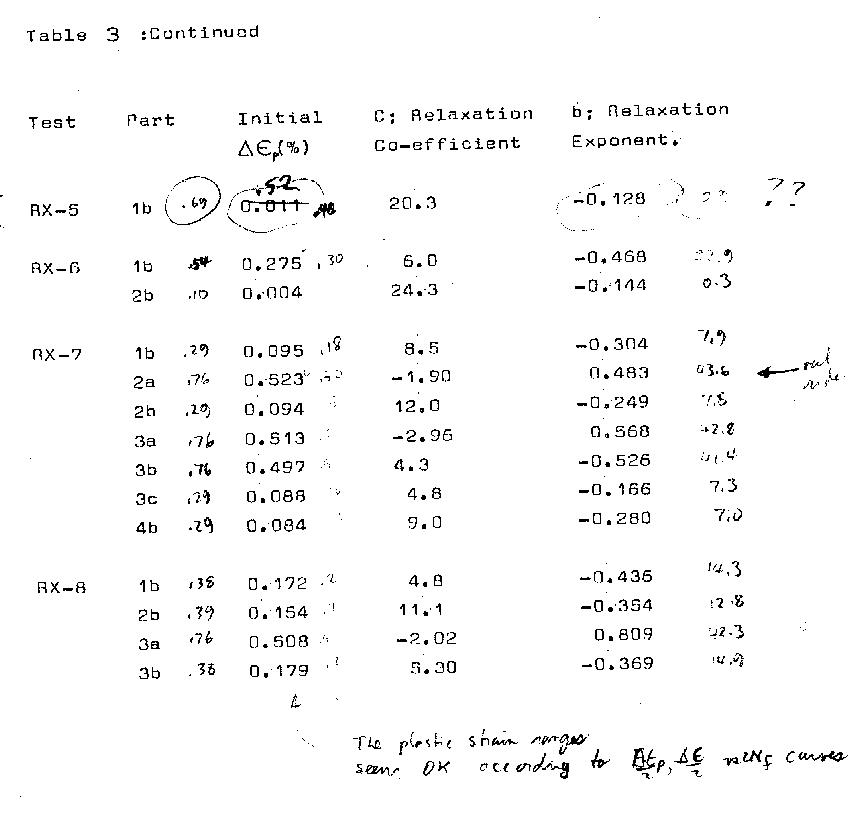
- Δεp Plastic strain range.
- ε₀ Mean strain
- ΔS Stress range
- So Mean stress
- |So| Absolute value of So
- So* Mean stress in first cycle of block
- b Mean stress relaxation exponent.
- |b| Absolute value of b
Introduction:
There are three areas, in the Low Cycle Fatigue Research program at the University
of Waterloo, where cyclic mean stress behaviour has become relevant:
- Micromechanisms: Andrewartha [1] is providing links between the areas of
material physics and mechanics by subjugating dislocation theories to
macroscopic tests. Mean stress is one of the variables.
- Cumulative damage criteria such as those of Smith et al [2] have found
that mean stress alters the fatigue life: better predictions of mean
stress behaviour will allow improved predictions of life.
- Simulations of hysteritic behaviour such as the computer models of
Martin et al[3] and the proposal of Jhansale[4], will eventually
incorporate the most feasible mechanisms and the damage theory to
provide means of predicting full scale structural fatigue response.
The present test series was directly related to the third area; the tests were
supervised by H.R.Jhansale, but it is thought that the data presented shall also
be of some use to the other two fields of investigation.
Previous work on the same subject for different
materials can be found in References [5] and [6]; the
test program being partially modeled on the work of Ref.[5].
Testing Program
The material investigated was
normalized mild SAE1015 steel (see Keshavan).
The chemical composition is given in Table 1.
Fatigue properties are described by Ref. [7].
Standard longitudinal specimens of 0.375" gage
length and 0.250" diameter were tested in an MTS
20 kip closed loop servo controlled system as described
in Ref. [8]. Conditioned output signals from load cell
and clip - on extensometer were recorded by both X-Y
plotter and high frequency response strip chart.
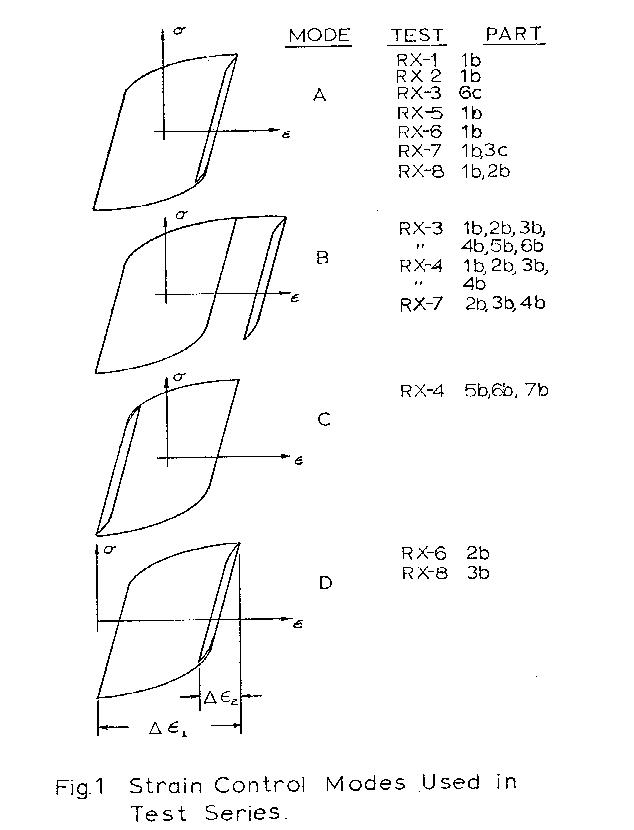
All eight specimens were subjected to strain
controlled deformation programs; characterized by a
block of cycles of large strain range ( Δε₁ ) followed
by a secondary block at a smaller strain range ( Δε₂ )
which "relaxed" the mean stress induced by the change
in strain limits. Typical hysteretic control conditions
for various parts of the test are shown in
Fig._1 and a sample strain/time and load/time
recording is given in Fig. 2.
The test program emphasized mean stress
relaxation behviour rather thatn the methods used to
induce it. For the normalized mild steel, which
displays hardening at high strain rages, and softening
in lower nonelastic regions, the relatively stable
strain range of Δε₁ = 0.77% was chosen for the "primary
cycling block" of six of the specimens, so as
to minimize hardening and softening effects on mean
stress relaxation. Two other tests, as listed in
Table 2 were conducted at the primary range of Δε₁=1.6%.
Secondary strain ranges varied from Δε₂=0.10%
to Δε₂=0.67%. In most tests the application of the
first two blocks of mean stress inducing ( labeled as 1a
for all tests), and means stress relaxing (block type 1b)
was followed by others at different ranges.
The notation used to denote primary blocks is as:
Part 1a, 2a, 3a ...etc.,
while secondary relaxation blocks are labeled:
Part 1b, 2b, 3b, ...etc.
Mean stress was taken as the average between
upper and lower stress limits for every second half
cycle and recorded as "mean stress per cycle".
Hardening and softening, taken as the change in stress
range were also recorded.
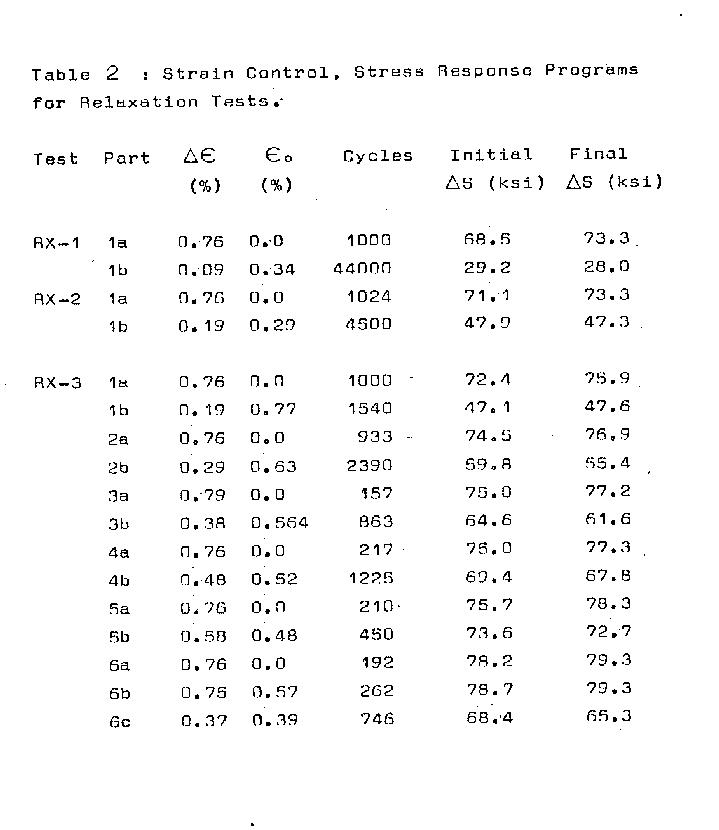
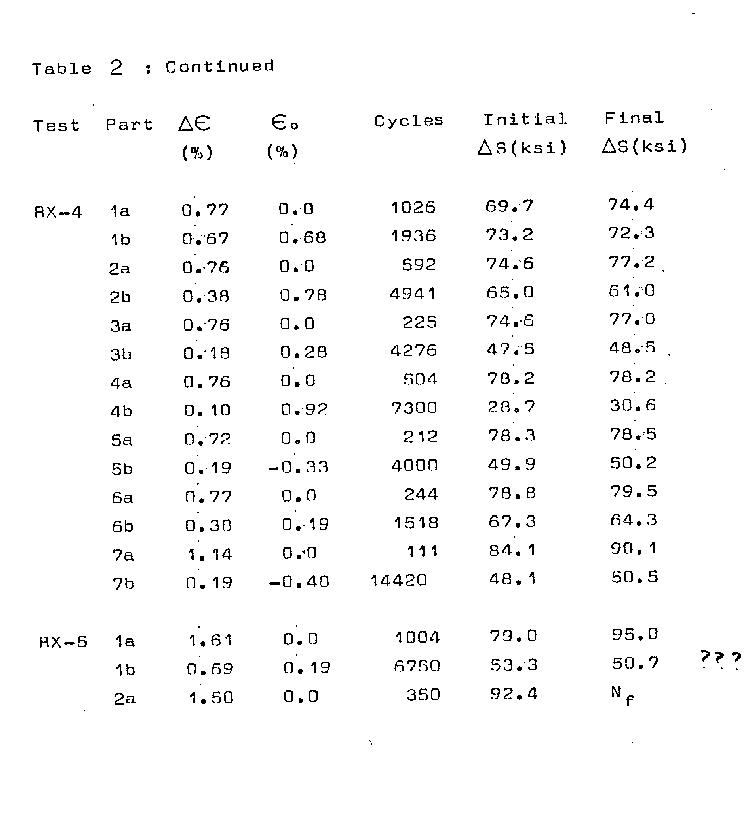
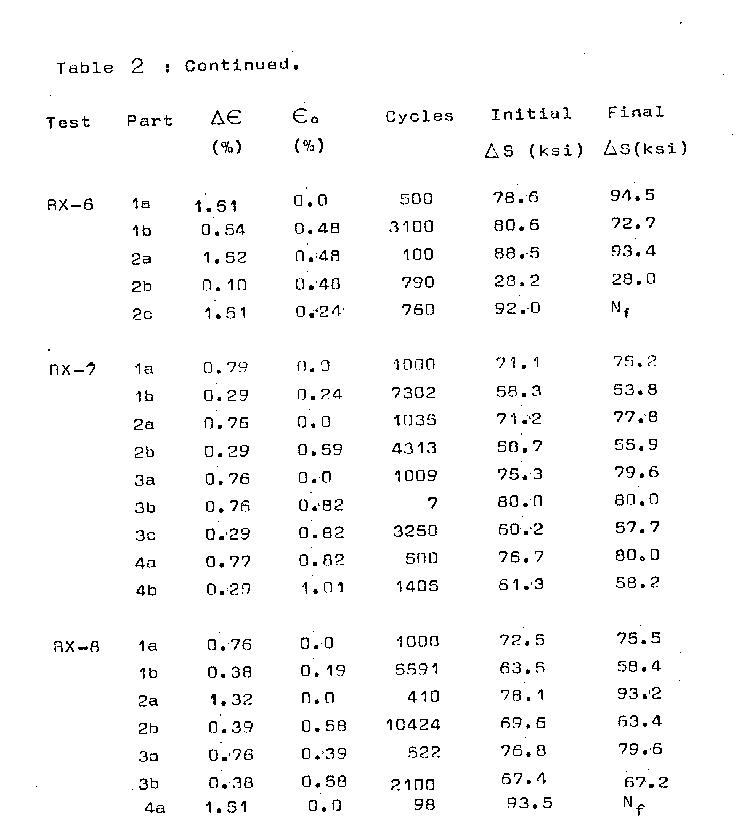
Results:
A history of all tests in terms of blocks,
strain ranges, initial stress range at the start of
the block and final stress range at the end of block
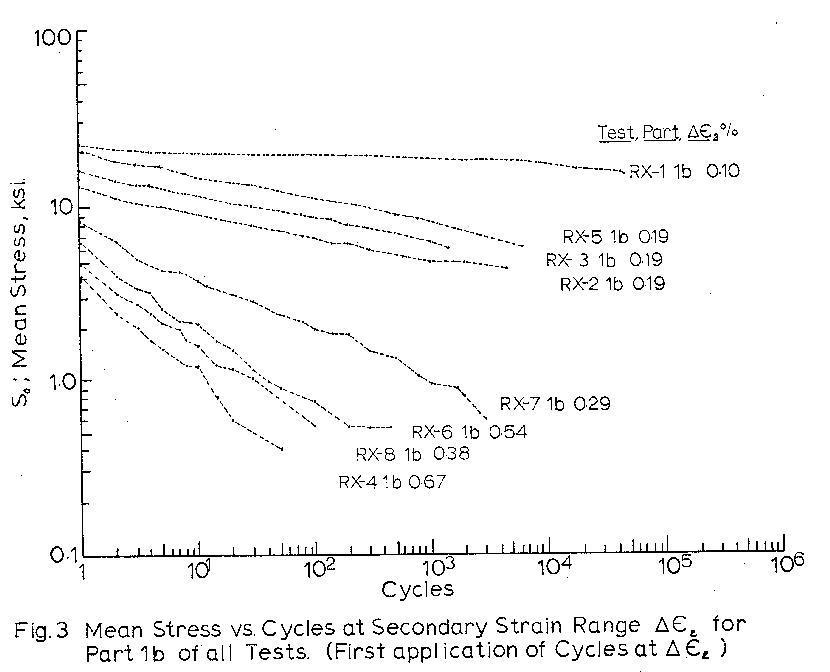
are given in Table 2. Mean stresses are recorded vs.
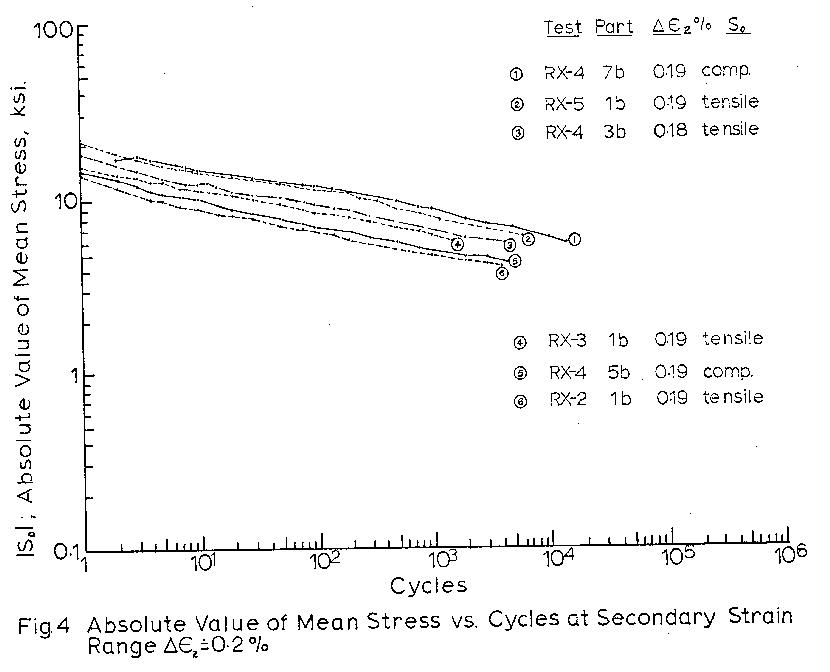
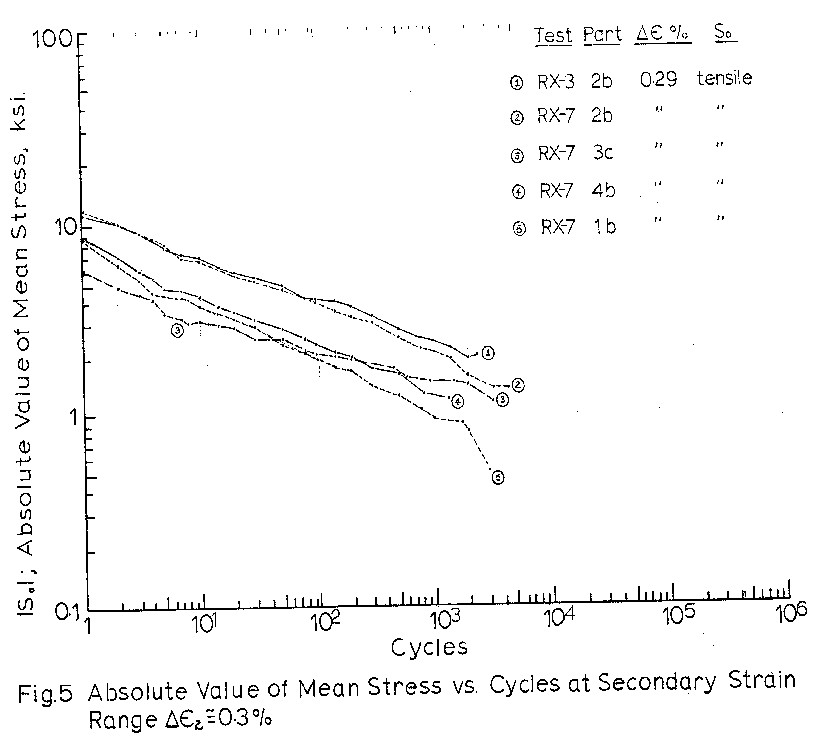
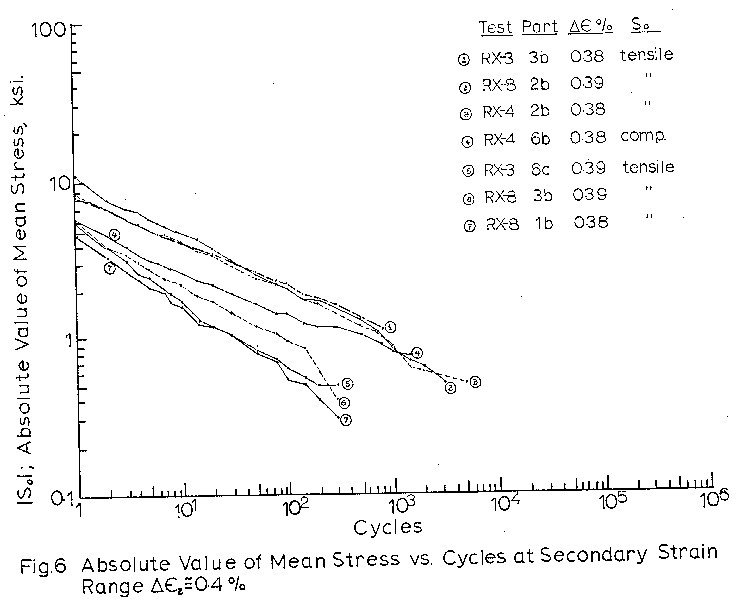
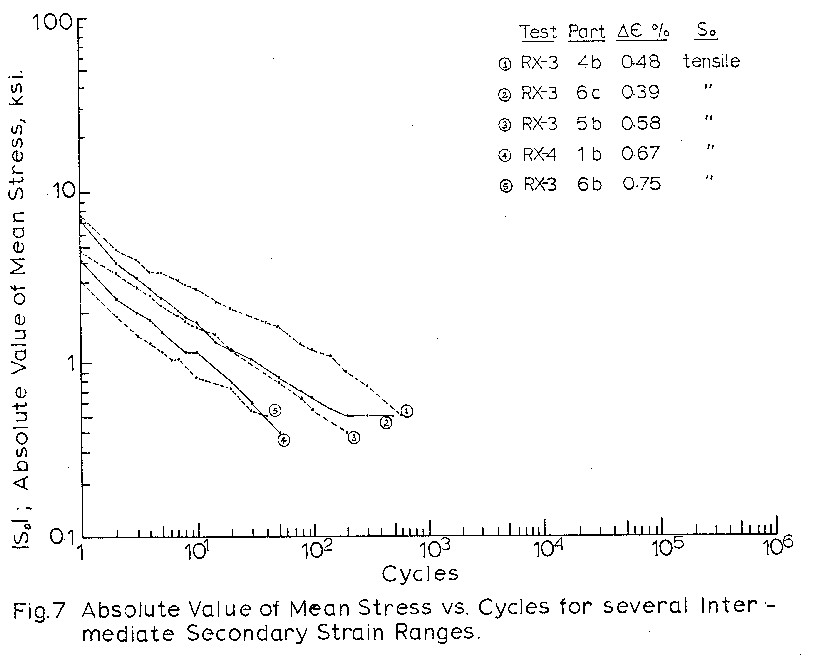
cycles for all 1b type blocks in Fig. 3, and separately
for test blocks of similar strain ranges and different
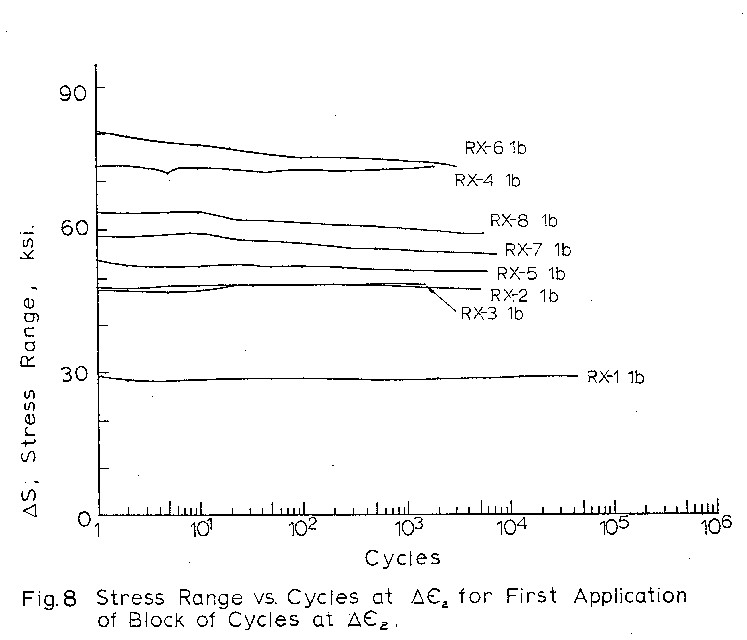
histories in Figs._4 and 7. Stress range vs. cycles
for type 1b blocks is given in Fig.8 to give some
indication of softening behaviour during mean stress
relaxation. Softening for the other blocks can be
determined from Table 2.
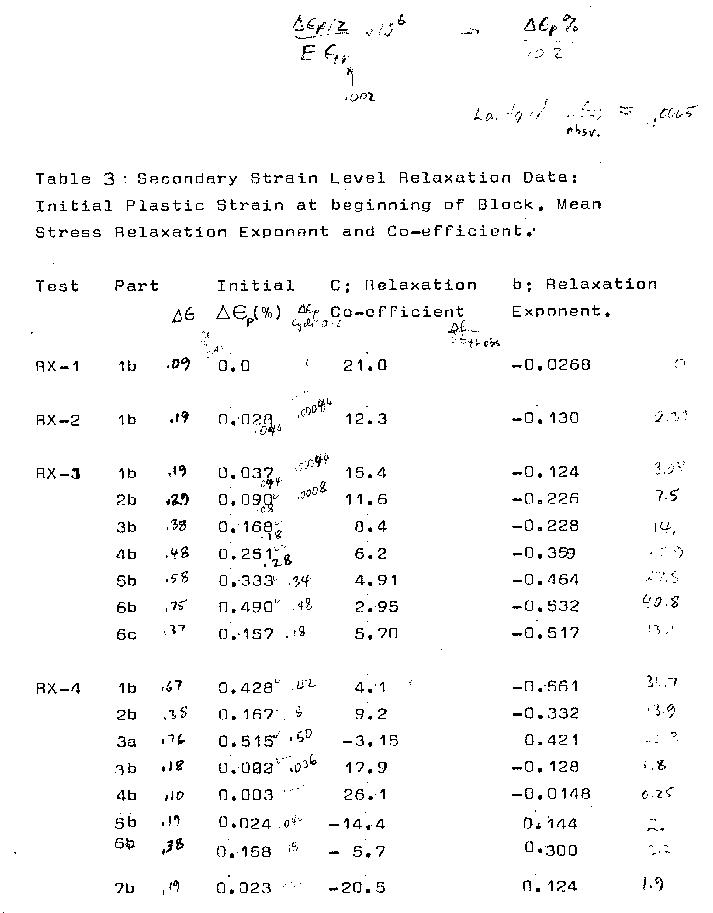
Figures 4 to 7 indicate that mean stress relaxation
as a function of cycles can be expressed as
So = C x Nb
where So is the mean stress at cycle N
C is the mean stress at cycle 1.
b is the slope of So vs. N on the log-log graph.
The exponents for all blocks with mean stress
relaxation are plotted vs. total strain range and
plastic strain range in Figs. 9 and 10 respectively.
The co-efficient appears to be related to the
loop shape of the primary strain limits and the
relative poition of the secondary strain limits.
Discussion:
From the test data it can be concluded that
mild steel in the "saturated" condition, where relatively
liitle hardening or softening occurs, relaxes
mean stress under strain cycling according to the
empirical equation:
So = C x Nb
The co-efficient, C is a function of the
relative poitiions of primary and secondary strain
ranges.
The exponent b, is believed to be related to
the plastic strain occurring in the secondary
block; as indicated by the trends in Figs._9 and_10.
Significant scatter is also evident in these figures;
specifically the exponents for tests RX-3 6c, and
RX-8_3a. Table 2 indicates that these recordings
were made fairly late in the life of the specimens
and it is possible that the presence of a crack has
affected the behaviour. This however cannot be the
only reason for the scatter as other tests at similar
lives still conform to the power relationship, without
the variation in exponents.
The effects of superimposed hardening or
softening behariour on mean stress relaxation are
difficult to interpret from present data. By
saturation of the material with 500 to 1000 cycles at an
intermediate strain range, it was hoped that large
changes in stress range with cycling, would not occur.
Table 2 indicates however that the mean stresses
were at times accompanied by some softening. One
possible way for cyclic hardening of softening, defined
as a change in stress range, to show up as
an apparent mean stress relaxation, is for the material
to become anisotropic with deformation. i.e. The
stress range in the tensile half cycle is always larger
or smaller than the stress range in the compressive
half cycle which immediately follows it. This would
result in a movement of the hysteresis loop along its
mean strain axis with cycling. Definite conclusions as
to this inter-relationship can however not be made
fro the results of the present study and further
research is warranted.
References:
- Andrewartha, F., MSc. Thesis, U. of Waterloo, 1970.
- Smith, K.N., P.Watson and T.H.Topper, "A Stress-Strain
Function for the Fatigue of Metals,"
Solid Mechanics Division, U.Waterloo, Oct. 1969.
- Martin, J.F., T.H.Topper, G.M.Sinclair, "Computer Based
Simulation of Cyclic Stress Strain Behavior," T.A.M. Report
No. 326, U.Illinois, Urbana
- Jhansale, H.R., Ph.D. Thesis, U.Waterloo, 1970.
- Topper, T.H., B.I.Sandor, J.Morrow, "Cumulative Fatigue
Damage under Cyclic Strain Control," J.Materials, V4 N1 March 1969.
- Morrow, J., G.M.Sinclair, "Cycle-Dependent Stress
Relaxation," ASTM Symp. on Basic Mechanisms of Fatigue,
ASTM Special Tech. Publ. No. 237.
- Keshavan, S., "Some Studies on the Deformation and
Fracture of Normalized Mild Steel under Cyclic Conditions,"
PhD Thesis, U.Waterloo, 1967.
- Butzow, G.N., R.W.Churchill, "Electrohydraulic Fatigue
Test Systems Capabilities," SESA Annual Meeting
Cleveland, Ohio, Oct. 28-30, 1964.